Mathematical Theory of Complex Calculus
- 04.06.2021
- 210
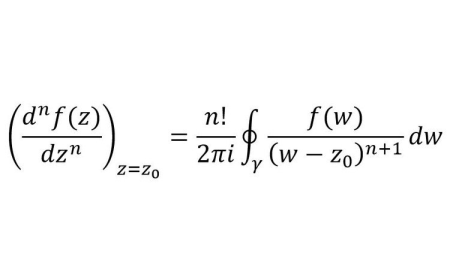
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz, 2 Ch
Genre: eLearning | Language: English + srt | Duration: 18 lectures (5h) | Size:3.48 GB
the Laurent series is mathematically derived.
Complex Calculus
How to derive the most important theorems and concepts related to Complex Calculus
Cauchy's integral theorem
Cauchy's integral formula
Laurent Series
How to derive the Fourier Series from the Laurent Series
How to derive the Taylor Series from the Laurent Series
Residues
Contour integration
Single Variable Calculus (especially: derivatives, integrals)
Multivariable Calculus (especially: Stokes' theorem, line integrals)
This course on Complex Calculus is structured as in the following:
the introduction focuses on the concept of complex functions;
the concept of derivative is extended to functions of a complex variable;
countour integration is discussed, and the following theorems are derived: Cauchy's integral theorem, Cauchy's integral formula;
Then, from Laurent, the Fourier and Taylor series are also derived;
residues are introduced and then used to do contour integration.
The prerequisites to the course are:
Single variable Calculus (especially derivatives and integrals);
Multivariable Calculus (especially line integrals and Stokes' theorem).
This course is based on the instructor's notes on Complex Calculus, and the presentation of the results is therefore original. The explanations are given by focusing on understanding and mathematically deriving the key concepts rather than learning the formulas and/or exercises by rote. The process of reasoning by using mathematics is the primary objective of the course, and not simply being able to do computations.
Some of the results presented here also constitute the foundations of many branches of science. For example, the Laurent series and the Residue Theorem, as well as the Fourier series, are staples in Quantum Mechanics, Quantum Field Theory, and also in Eeering (in the Control theory of dynamical systems for instance).
Students interested in the concepts of Complex Calculus
Students who want to rigorously derive the concept of Fourier Series
Students who want to understand how to do contour integration
DOWNLOAD
uploadgig
https://uploadgig.com/file/download/760eE37c3c809Deb/y8ZuZKYI__Mathematic.part1.rar
https://uploadgig.com/file/download/955623Ea71C088E2/y8ZuZKYI__Mathematic.part2.rar
https://uploadgig.com/file/download/4E27940c3d1a19Fb/y8ZuZKYI__Mathematic.part3.rar
https://uploadgig.com/file/download/98A30742460aed38/y8ZuZKYI__Mathematic.part4.rar
rapidgator
https://rapidgator.net/file/96198941f520becb5bb636d913a4cd7b/y8ZuZKYI__Mathematic.part1.rar.html
https://rapidgator.net/file/59a896a40825a853cd7942e7a2c77283/y8ZuZKYI__Mathematic.part2.rar.html
https://rapidgator.net/file/ae4e898f95d857ce2176f071a8f5c084/y8ZuZKYI__Mathematic.part3.rar.html
https://rapidgator.net/file/3d36de614fe642b502ffb45f8ea142fc/y8ZuZKYI__Mathematic.part4.rar.html
nitro
https://nitro.download/view/958E24ABFC6F3D8/y8ZuZKYI__Mathematic.part1.rar
https://nitro.download/view/0267A6A377699B0/y8ZuZKYI__Mathematic.part2.rar
https://nitro.download/view/BFA184F7D81B58C/y8ZuZKYI__Mathematic.part3.rar
https://nitro.download/view/9896B27DBC73C12/y8ZuZKYI__Mathematic.part4.rar